几何矢量的内积
编辑“本词条基于小时百科相关页面[1]”
1 几何定义编辑
我们先来看内积的几何定义.注意该定义不需要任何坐标系的概念.
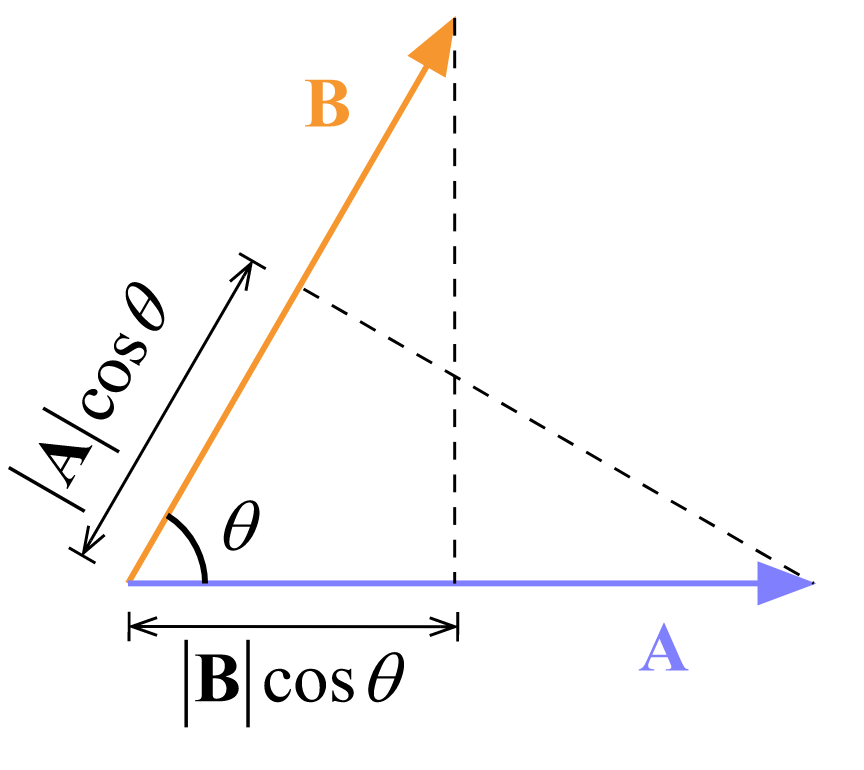
如图 1 ,两个几何矢量的内积(inner product)[2]就是把它们的模长相乘,再乘以它们的夹角的余弦值.一般用一个实心圆点表示几何矢量的内积(不可省略):

 是两个矢量的夹角.注意两个矢量内积得到的是一个标量.几何定义中(图 1 ),既可以把内积理解为
是两个矢量的夹角.注意两个矢量内积得到的是一个标量.几何定义中(图 1 ),既可以把内积理解为 投影在
投影在 上的模长乘以
上的模长乘以 的模长,也可以理解为
的模长,也可以理解为 投影在
投影在 上的模长乘以
上的模长乘以 的模长[3].可见当两矢量模长不变时,若方向相同,内积取最大值
的模长[3].可见当两矢量模长不变时,若方向相同,内积取最大值 ;若方向相反,内积取最小值
;若方向相反,内积取最小值 ;若相互垂直,则内积为 0.
;若相互垂直,则内积为 0.我们说两个内积为 0 的矢量互相垂直(perpendicular),或者说正交(orthogonal).几何矢量与自身内积可得该矢量模长的平方.单位矢量与自己的内积等于 1.把一个矢量除以自身模长得到同方向单位矢量的过程叫做矢量的归一化(normalization).
3 内积的坐标运算编辑
若已知,
在平面直角坐标系
中坐标分别为
和
,那么如何用坐标表示内积运算的结果呢?先用正交归一基将两矢量展开
所以
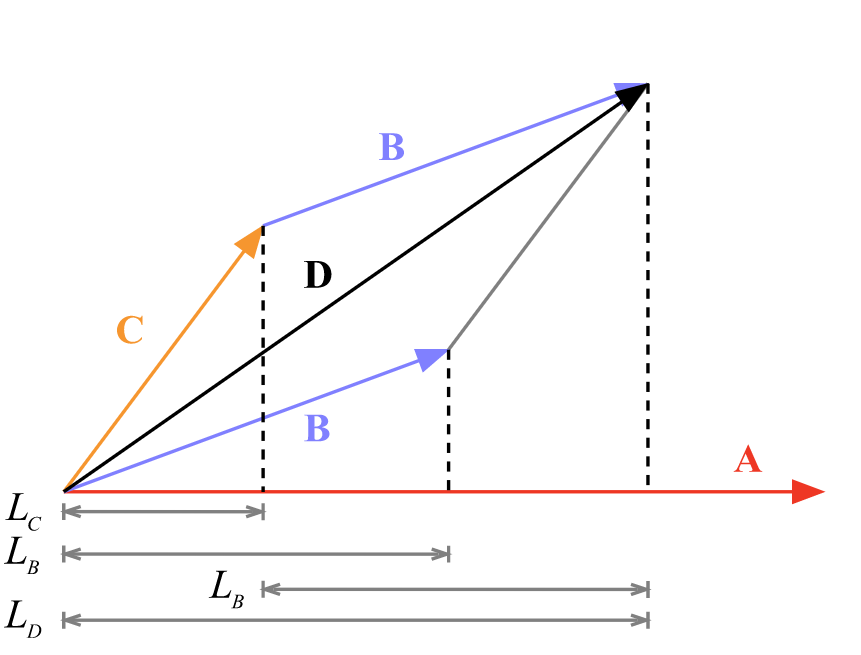
4 证明内积的分配律编辑
如图 2 ,令![]() ,把
,把![]() ,
,![]() ,
,![]() 分别用几何定义理解为
分别用几何定义理解为![]() ,
,![]() ,
,![]() 在
在![]() 上的投影乘
上的投影乘![]() ,且令投影长度分别为
,且令投影长度分别为![]() .那么要证明
.那么要证明![]() ,只需证明
,只需证明![]() 即可.现在把
即可.现在把![]() 平移使其起点与
平移使其起点与![]() 的终点对接(投影长度不变).从图中立即得出
的终点对接(投影长度不变).从图中立即得出![]() .
.
 ,把
,把 ,
, ,
, 分别用几何定义理解为
分别用几何定义理解为 ,
, ,
, 在
在 上的投影乘
上的投影乘 ,且令投影长度分别为
,且令投影长度分别为 .那么要证明
.那么要证明 ,只需证明
,只需证明 即可.现在把
即可.现在把 平移使其起点与
平移使其起点与 的终点对接(投影长度不变).从图中立即得出
的终点对接(投影长度不变).从图中立即得出 .
.参考文献
阅读 296
版本记录
暂无